This is my first post about cryptography. Recently I learnt basics about public key encryption and the TLS handshake. But the key exhange in the TLS handshake inspected by Wireshark, i.e. ECDH(Elliptic-curve Diffie–Hellman) troubled me for a while. This this the first time I knew Elliptic curve. After some investigation, I’m recording those knowledges in case that I forget them.

Note: in the following several posts, I would record more things I learnt about cryptography and its application in the computer network and Internet.

First glance

A elliptic curve could be defined as:

$$y^2 = x^3 + ax + b$$

where

$$4a^3 + 27b^2 \ne 0$$

Some examples of elliptic curves are like:

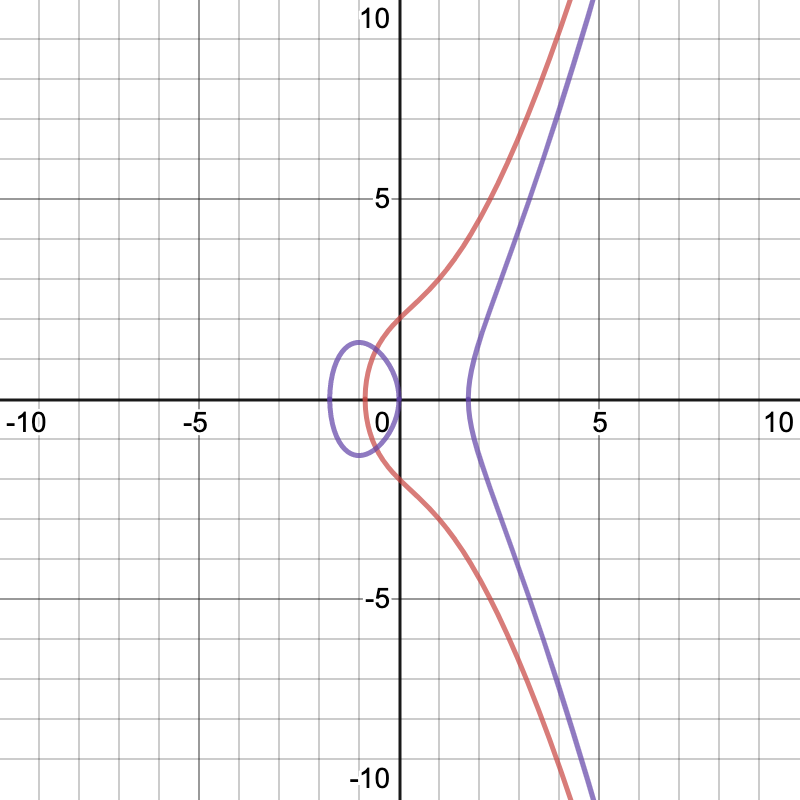
equation for red line is $y^{2}=x^{3}+4x+4$, equation for purple line is $y^{2}=x^{3}-3x$

Group

Now lets review the Group) concept.

A set $G$ is a group if a binary operation could be defined on it, and 4 conditions are met. Usually we denote the operation as addition and denoted as $\oplus$, then the 4 conditions are:

1. Closure: $m \oplus n$ is always in $G$ as long as $m$ and $n$ in $G$.
2. Associativity: for any $m$, $n$ and $r$ in $G$, $(m \oplus n) \oplus r = m \oplus (n \oplus r)$.
3. Identity element: there is an element $\circledcirc$ in $G$ such that $m \oplus \circledcirc = \circledcirc \oplus m = m$ for any $m$ in $G$.
4. Inverse element: for any $m$ in $G$, there is an element $n$ in $G$ such that $m \oplus n = \circledcirc$, and we say $n = \ominus m$.

A group is a Abelian group if the follwoing condition is also met:

commutation: for any $m$ and $n$ in $G$, there is $m \oplus n = n \oplus m$

Aparently the set of all real numbers $R$ could be an Abelian group with the arithmetic adding operation.

Finite group

A finite group is a group with limited elements. For any element $m \ne \circledcirc$ in a group $G$, if you repeatly add $m$ to itself, you would get $G$. I.e. there is a number $d$ such that $dm = \circledcirc$.

Why? Lets say the group has $n$ elements, then the list $m, 2m, 3m, ..., (n+1)m$ would have same elements in it. Assume they are $xm = ym$, then you see $(x-y)m = \circledcirc$.

Define group on the elliptic curves

First, the set consists of all points in a elliptic curve.

The Identity element $\circledcirc$ would be a little special, it’s defined as the infinitely far points of the curve.

Now, lets define the operation. For any points $m$ and $n$ in the curve:

1. if $m = n$ and $y_m = 0$, then $m \oplus n = \circledcirc$
2. if $m = n$ and $y_m \ne 0$, then $\ominus (m \oplus n)$ is the other intersection of the curve and the line tangent to the curve in $m$.
3. if $m \ne n$ and $x_m = x_n$, then $m \oplus n = n \oplus m = \circledcirc$
4. if $m \ne n$ and $x_m \ne x_n$, then $\ominus (m \oplus n)$ is the 3rd intersection of the curve and the line cross $m$ and $n$.

From the 3rd and 4th cases above, we know the relation between $m + n$ and $m$, $n$ would be like:

It can be proved that such a group is an Abelian group.

Scalar multiplication

We can also defin a scalar multiplication based on the plus operation upon the elliptic curve groups:

$$dm = \sum_{i=1}^d m$$

where $d$ is a positive integer and $m$ is a element in the group.

The above expression could be calculated in time complexity of $O(logd)$ by disassembling the $d$ into factors that are powers of 2.

The logrithm problem

In last section, we see given $d$ and $m$, it’s easy to get $dm$. However, given the $m$ and result of $dm$, with some cleverly constructed instances it would be very hard to know the value of $d$, i.e. the times of operation performed to get the $dm$. And this hard problem is called logrithm problem.

Ring

An Abelian Group is a Ring if multiplication denoted as $\otimes$ could also be defined and:

1. associative: $(a \otimes b) \otimes c = a \otimes (b \otimes c)$ for any $a$, $b$, $c$ in the set.
2. distributive: $a \otimes (b \oplus c) = (a \otimes b) \oplus (a \otimes c)$ and $(b \oplus c) \otimes a = (b \otimes a) \oplus (c \otimes a)$.
3. multiplicative identity 1: $a \otimes 1 = 1 \otimes a = a$.

Note, a ring is a commutative ring if multiplication commutative is is satisfied.

Field

A Field) is a commutative ring which also satisfies:

1. additive identity $\circledcirc$ is different from multiplicative identity $I$.
2. multiplicative inverse element, for any $m \ne \circledcirc$, there is $n$ such that $m \otimes n= I$, in which we mark $n = m^{\ominus 1}$, hence division could be defined: $a \div b = a \otimes b^{\ominus 1}$.

Finite field on prime

For a prime $P$, the set of integers from 0 to $P-1$ could be a field. And the addition and multiplication are defined as:

$$m \oplus n = (m+n)\mod P$$ $$m \otimes n = (mn)\mod p$$

Besides, assume the number 0 and 1 are $\circledcirc$ and $I$ respectively. Then apparently $\ominus m$ is $P - m$ since:

$$(m + (P-m)) \mod P = 0$$

But the multipilicative inverse is not that easy, actually the extended Euclidean algorithm tell us this could be done in time complexity of $O(logP)$. As an example, 4 and 2 are mutual multipilicative inverse when $P$ is 7 since $4 \times 2 \mod 7 = 1$.

Elliptic curve over finite fields

Previously the elliptic curves consist of points with coordinates of real numbers. But now we restrict the curve upon a finite field which only contains integers betwen 0 and $P-1$.

$$y^2 \equiv x^3 + ax + b \mod P$$

When

$$4a^3 + 27b^2 \not\equiv 0 \mod P$$

Where $P$ is a prime number, $x$, $y$, $a$ and $b$ are integers, and $0\le x, y\le P-1$.

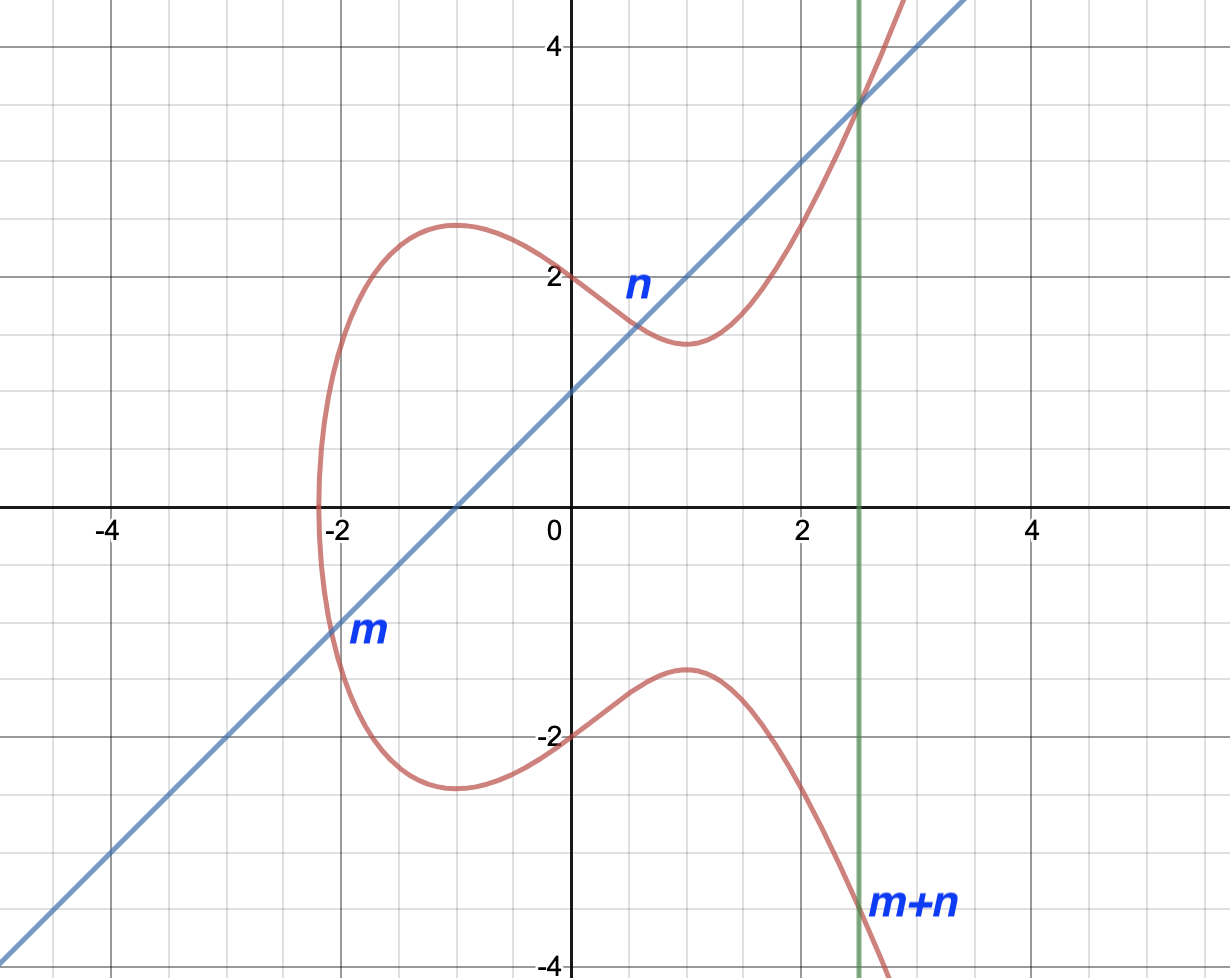
Here is an example graph of $y^2 \equiv x^3 - 7x + 10 \mod 19$:

Note that most of the points in the above graph are symmetrical over the line $y=P/2$ except the points on line $y=0$.

Group on the elliptic curve over finite fields

To define a group, firstly we need to define the plus operation on the elliptic curve over finite fields. The plus operation is similar to the operation we defined previously for elliptic curve over real numbers.

The identity element is same as before. The reverse pair of elements are symmectircal over the line $y = P/2$.

For any pointers $m$ and $n$ on the discrete curve and $x_m \ne x_n$, $m \oplus n$ is the reverse proint of the 3rd intersection between the discrete curve points and the lines denoted by:

$$ax + by + c\equiv 0 \mod P$$

when one of the lines cross $m$ and $n$, and $a$, $c$ and $c$ are inetger constants.

The following is an example, where the discrete elliptic curve equation is $y^2 \equiv x^3 - 7x + 10 \mod 19$, and the lines equation is $y \equiv 2x \mod 19$:

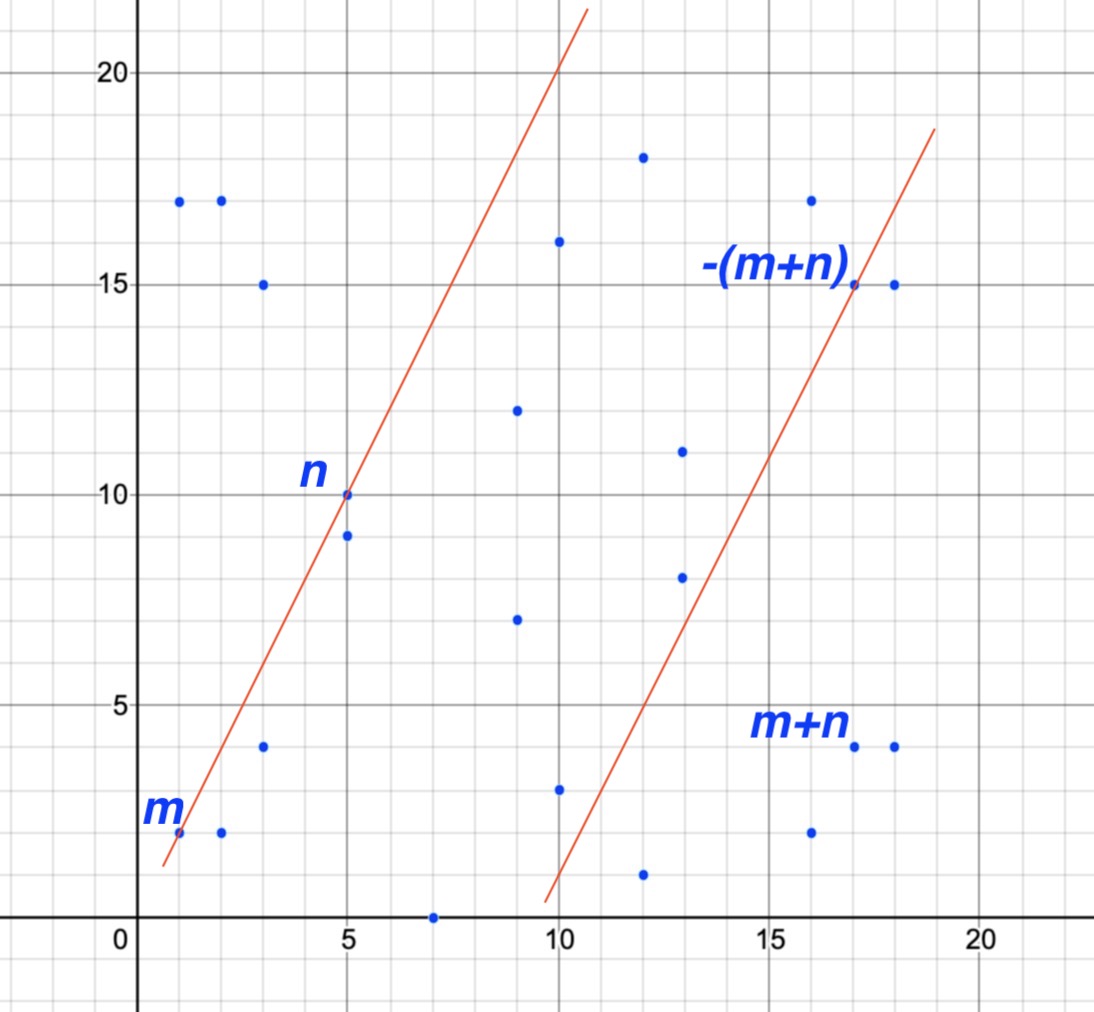
In above diagram, $m$ and $n$ are $(1, 2)$ and $(5, 10)$ respectively, while $m \oplus n$ is $(17, 4)$. So this is a general example, how about when $m$ is just $n$? What’s the $\circledcirc$ is this group?

The $\circledcirc$ is still the infinitely far point. Well, this seems strange becase the infinitely far point is not in the discrete elliptic curve. And there has $m \oplus n = \circledcirc$ when $x_m = x_n, y_m \ne y_n$.

When $m$ is just $n$, we can also get the tangent line whose slope value is the derivative of the elliptic curve equation at the point $m$.

It could be proved with such a plus operation defined, a group is generated on the discrete elliptic curve over a finite field from prime $P$.

The number of points (including the $\circledcirc$) in such a group is called the order of the group. The Schoof’s algorithm is an efficient algorithm to calculate the number of points.

Similar with previous continuous elliptic curve, we can perform scalar multipilication:

$$dm = \sum_{i=1}^d m$$

where $d$ is a positive integer and $m$ is an element in the group.

For any $m$ in such a group $G$, the smallest integer $d$ such that $dm$ equals $\circledcirc$ is called the order of the subgroup which consists of $\circledcirc$, $m$, $2m$, $3m$, …, $(d-1)m$. The subgroup is cyclic. And the number of elements in a subgroup is called order of the subgroup.

Let’s say the order of the parent group is $D$. According to Lagrange’s theorem), the order of a subgroup is a diviser of $D$.

As an example, lets use the $y^2 \equiv x^3 - 7x + 10 \mod 19$ and assum3 $m$ is $(1, 2)$. It could be calculated that $m, 2m, 3m, 4m, 5m, 6m, 7m, 8m$ are $(1, 2), (18, 15), (9, 12), (7, 0), (9, 7), (18, 4), (1, 17), \circledcirc$. Show as below:

In above diagram, the order of the parent group is 24. The order of the subgroup is 8, which is a diviser of 24. Also for the point $(7, 0)$, its inverse point is itself (actually the slope value here is infinity).

Note that different subgroups might share points. For instance, in the above example any subgroup whose base point is $m$ order is an even number $s$, then $\frac{s}{2}m$ is the point $(7, 0)$.

Hence for any $m$ in the parent group, we can check the divisers of $D$ one by one to find out the order of subgroup based on $m$.

On the contrary, for any prime diviser $d$ of $D$, any element point $m$ such that $(D/d)m$ not equal the $\circledcirc$ is the base point to form a subgroup whose order is $d$. (Hint: $Dm$ is always the $\circledcirc$.)

Given $m$ and $n$ in such a group G, getting a $k$ such that $km=n$ is also very hard for some instances of discrete elliptic curve, just like the logrithm problem we mentioned previously.

Elliptic curve cryptography applications

To leverage elliptic curve group over finite fileds on primes, there are some parameters called domain parameters to determine the concrete elliptic curve instances.

1. $a$ and $b$, real numbers to determine the $y^2 = x^3 + ax + b$ equation.
2. $p$, a prime that determine the finite field of 0, 1, 2, 3, …, $p-1$ .
3. $G$, a base point in the discrete elliptic curve to form a cyclic subgroup of $G$, $2G$, $3G$, …, $\circledcirc$.
4. $n$, which is order of the subgroup based on $G$, hence $nG$ is the $\circledcirc$.
5. $h$, called cofactor, which is result of $n$ divides the order of the parent group.

The above $(p, a, b, G, n, h)$ consists the domain parameters that determine the concrete instances. Thoso domain parameters are public to everyone.

In the Elliptic curve cryptography, The private key is a random number $d$ such that $1 \le d \le n-1$. The public key is the result of $dG$.

EC Diffie-Hellman key exchange algorithm

In EC Diffie-Hellman key exchange algorithm. Alice and Bob have their private keys $d_A$ and $d_B$. With the public domain parameters, they would compute $d_A G$ and $d_B G$ and exchange these two values (public keys). Finally, they would compute $d_A d_B G$ and $d_B d_A G$ respectively as the secret key for symmetric encryption. Of course $d_A d_B G = d_B d_A G$.

The EC Diffie-Hellman key exchange is based on that given the domain parameters, it’s hard to know $d_A d_B G$ given $d_A G$ and $d_B G$, and same for $d_A$ and $d_B$.

While the original Diffie-Hellman key exchange algorithm is based on exponential modular. Assume $p$ is a prime and $k$ is a primitive root modulo $p$ and both of them are public. Private keys are random numbers $d_A$ and $d_B$, public keys are $k^{d_A} \mod p$ and $k^{d_B} \mod p$, and the secret key for symmectric encryption is $k^{d_A d_B} \mod p$.

The shared secret key in EC Diffie-Hellman key exchange algorithm are coordinates of the point $d_A d_B G$, which could be used to perform symmectirc encryption just like TLS does.

Actually in TLS, we often see ECDHE in which the ending E means ephemeral which means the shared secret key is temporary. Actually when TLS uses ECDHE, during the handshake procedure, the public and private keys generated in ECDHE won’t be used for encryption. TLS just want both sides to generate a shared private symmectric encryption key, which is really for encryption of application data.

EC digital signature algorithm

EC digital signature algorithm is a signature algorithm like RSA. Alice could use her private key $d_A$ to generate a signature for digest of a message. Bob would be able to verify the signature by using public key of Alice, i.e. $d_A G$.

ECC and RSA

ECC(clliptic curve cryptography) is better than RSA in that key size of ECC is smaller to achieve same security level. Moreover, the security level improved by doubling key size of RSA is less than ECC.